梯度下降法(8) -- Activation Function

neural network tensorflow gradient descent

I code so I am 2025-06-15 00:02:37 ‧ 776 瀏覽

分享至

Activation Function是將線性迴歸轉換為非線性函數，使神經網路更具通用性(Generalization)，類似Kernel PCA及Kernel SVM，這是機器學習將線性模型轉換為非線性函數常用的方法。Activation Function被直譯為『激勵函數』，不能表達真正的意義，故以下介紹直接使用Activation Function。

Activation Function 簡介

TensorFlow官網首頁模型建構的程式碼如下：

model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  tf.keras.layers.Dense(10, activation='softmax')
])

其中第1個Dense參數activation='relu'，表示完全連接層(Dense)後面連接ReLU Activation Function，也可以寫成：

  tf.keras.layers.Dense(128),
  tf.keras.layers.ReLU(),

第2個Dense參數activation='relu'，表示完全連接層(Dense)後面連接Softmax Activation Function，也可以分兩行撰寫。

神經網路中間的隱藏層常使用ReLU Activation Function，最後一層則會使用Softmax Activation Function，原因如下：

ReLU函數為 f(x) = max(0, x)，即過小的數值一律忽略，類似在腿上輕輕打一下，神經傳導系統可能會忽略此外界刺激，大腦不會作出反應，須要特定力道以上，才會有所反應。早期建議使用Sigmoid Activation Function，後來發現使用ReLU效果更好，但是有些狀況會採用其他的Activation Function。
最後一層常會使用Softmax Activation Function，將輸出轉會為機率格式，便於判別何者為最大值，即當作預測的類別，所謂機率格式是每個輸出值均介於[0, 1]之間，所有輸出值總和會等於1。注意，輸出值不代表預測的機率或可信度，它只是一個預測的排序(Ranking)而已，例如使用辨識手寫阿拉伯數字(0~9)的模型進行推論，若我們輸入『A』，模型輸出值還是會有一個值特別大，事實上『A』並不是0~9中任何一個數字。

Activation Function 類別

可以參考維基百科Activation Function說明，內文有一列表，部份截圖如下：

欄位包括Activation Function名稱、函數繪圖、公式、一階導數、範圍及連續性。

以sigmoid為例，公式如下：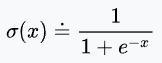

若原來模型是 y = wx + b，經過轉換將x置換為wx + b，公式如下：

TensorFlow提供更多的Activation Function，可參閱Keras說明或TensorFlow說明。

實作

範例1. 將TensorFlow官網首頁的範例拿掉Activation參數，測試其影響。

拿掉第1個Dense 的 Activation參數：

model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(128),
  tf.keras.layers.Dropout(0.2),
  tf.keras.layers.Dense(10, activation='softmax')
])

重新訓練，結果準確度只有0.91，少了0.06。
拿掉第2個Dense 的 Activation參數：

model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  tf.keras.layers.Dense(10)
])

重新訓練，結果準確度只有0.15。
拿前10筆為例，顯示輸出值及找出最大索引值。

pred = model.predict(x_test[:10], verbose=False)
for i in range(10):
    print(f'pred={pred[i]}, max={np.argmax(pred[i])}')

重新訓練，結果與加了Softmax Activation Function，預測結果差異很大。

未加Softmax Activation Function。
加了Softmax Activation Function。

KAN(Kolmogorov-Arnold Networks)

由於Activation Function有非常多種，如果沒有一一試過，很難知道特定訓練資料適合使用哪一種Activation Function，因此，在2024年5月有一篇論文【KAN: Kolmogorov-Arnold Networks】曾引發廣泛的討論，作者試圖直接以貝茲曲線(B-spline curve)取代Activation Function，直接訓練模型，找出控制點最佳值，亦即直接求解非線性函數，但經過一段時間後討論熱度就冷卻下來了，筆者認為神經網路的重點不在Dense，而是其他的神經層，例如卷積層(Convolution)，將輸入像素轉換為線條，又如嵌入層(Embedding)將文字轉換為實數向量，RNN考慮上下文(Context)，重點在於特徵工程(Feature engineering)。KAN的詳細介紹可參閱筆者撰寫的『Hello KAN, 建構深度學習模型的另一種思維』。